| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 여행계획
- 일상탈출
- Transition
- 일상회피
- bytecode 분석
- Android
- 보안
- 버킷리스트
- 취약점
- 치유
- Recylcer
- opcode
- javap
- Interface
- bytecode
- 심리여행
- Shared Elements
- Navigation Component
- ㅇ
- IMPLEMENT
- 여행
- HelloWorld
- extends
- 심리학
- 회피
- static
- throws
- abstract
- 보안취약점
- jvm
- Today
- Total
패스트터틀
(basic) dp, bitmask, lis... 본문
본 포스팅은 블로거가 개발언어의 개념정리 필요를 위한것입니다.
목차와 차례가 뒤죽박죽이며 오직 블로거의 편의목적을 위해 작성되었음을 알려드립니다.
- dp
- bitmask
- lis
- dp
dp = dynamic programming 의 약자로 단어자체와 개념은 전혀 연관이없으며
쉽게말해서 기억하며 프로그래밍하는것이다.
예를들어서
fibonacci 수열을 구할때
다음과 같이 코딩을 할수있다. 예를들어서
int dp(int x){
if(x==1) return 1;
if(x==2) return 2;
return dp(x-2) + dp(x-1);
}
int main(){
cout << dp(10) ; //
}하지만 이런식으로 코딩을 해볼경우 10까지는 무난하나 더 큰숫자를 넣을경우 엉청나게 오랜시간이 걸리는데
이유는 다음과 같다.
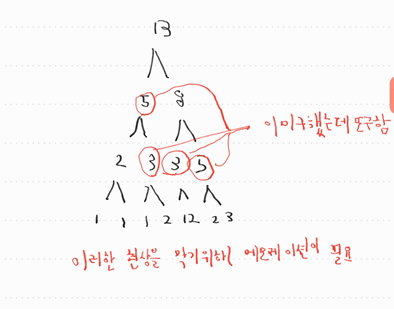
반복적으로 이미 구한 계산을 다시 구하려고 한다.

분할정복 기법으로 짤경우 높이가 2^n 만큼 커지기 때문이다. 예를들어서 dp(100)을 입력할경우
컴퓨터는 2^100 에 해당하는 높이를 계산해야된다.
결국 컴퓨터는 계산하는데 엉청난 시간이 필요하게 된다.
이러한 것을 방지하기 위해서 이미 구한것은 또 다시 계산하지 말자 라는 의미에서 이미 구한것은 값을 따로 저장해놓는것을 추가한다면 다음과 같이 코드를 짜볼수있다.
int d[100];
int dp(int x){
if(x==1) return 1;
if(x==2) return 2;
if(d[x] != 0) return d[x];
return d[x] = dp(x-2) + dp(x-1);
}
int main(){
cout << dp(10) ; //
}이런식으로 처리할경우 다음과같이 볼수있다.

1부터 계산해서 올라갈경우
왼쪽은 O(2^n)이지만 오른쪽은 값을 저장하기 때문에 다시 계산할필요가 없어져 O(n)으로 줄어든다.
dp문제는 규칙성으로 하여금 점화식으로 새우는것이 제일 중요하다.
- bitmask
{1,2,3,4,5,6,7,8,9} 이런식으로 있을때
여기서 부분집합을 고른다고 칠때 1과 6과 7을 골라서 {1,6,7}을 만든다고 정한다면
비트로 다음과 같이 표현할수있다.
{1,6,7} => 001100001
그리고 다음과같이 연산하여서 추가 삭제 확인을 할수있다.
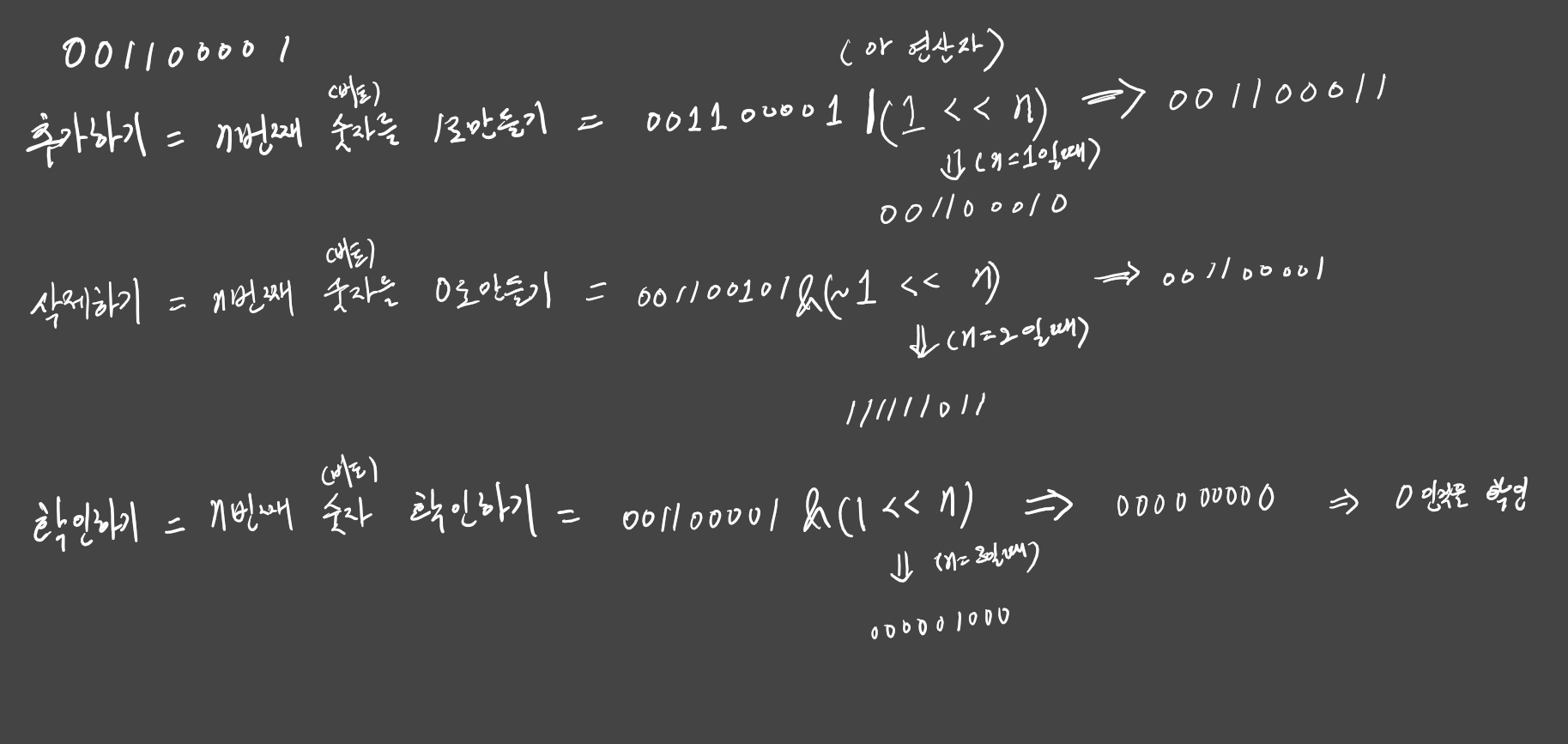
- lis
lis = Longest Increasing Subsequence(LIS) 의 약자이다.
최장 증가 수열이다.
'Algorithm > #define' 카테고리의 다른 글
| (basic) Dijkstra, Floyd warshall (0) | 2020.01.08 |
|---|---|
| (basic) Searching Linear, Binary(upper,lower bound) (0) | 2019.12.12 |
| Recursive call (재귀) 함수에 관하여 (0) | 2019.12.05 |
| (basic) recursive call,stack,queue, dfs,bfs .... (0) | 2019.11.11 |
| (basic) 시/공간 복잡도, 빅오(big-O), 트리, 정렬 알고리즘(코드포함) (0) | 2019.10.14 |




