| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- javap
- bytecode 분석
- jvm
- throws
- Shared Elements
- Navigation Component
- 일상회피
- static
- opcode
- 심리여행
- extends
- IMPLEMENT
- 취약점
- Recylcer
- 일상탈출
- Interface
- 여행
- 심리학
- 보안
- abstract
- 버킷리스트
- ㅇ
- 치유
- HelloWorld
- 여행계획
- bytecode
- 회피
- 보안취약점
- Android
- Transition
- Today
- Total
패스트터틀
(Baekjoon) dp - (7) 가장 긴 증가하는 부분 수열_O(N^2) 본문
https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
www.acmicpc.net
LIS = Longest Increasing Subsequence, 최장증가수열이다.
주어진 값에서 증가하는 수의 집합들중 가장 큰 원소의 개수를 구하는 방법에 관한 문제이다.
어떠한 알고리즘이 해당문제를 푸는데 최적화된 알고리즘인것을 보장할수있는것은 어떻게 알수가 있을까?
문제를 풀다보니 회의감이 든다. 마치 LIS라는 문제라서 LIS로 풀고 DP문제라 DP로 풀고 어떠한 알고리즘이랑 주제에 맞춰서 해당 주제이기때문에 해당 LIS DP 등 해당 알고리즘이 타당한것처럼 보인다.
하지만 이런 알고리즘이 타당한지 타당하지 않는지에 대한 확인은 누가해줄수있는것인가?
문제를 푼사람들은 많지만 전부다 직감에 의해 또는 이러이러할것같아서 하는식으로 시작하여서
마치 그것이 정답인것마냥 코딩을 한 사람들이 많다.
하지만 이것이 정답인지 아닌지랑 상관없이 과정이 타당한것임을 확인해주는것은 누가해줄수있는가?
이상 그냥 생각해본것이고
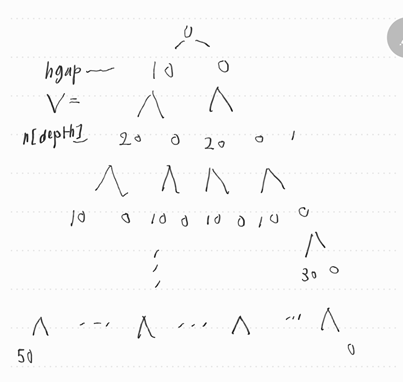
이런식으로 풀려고 했으나 시간초과가 되었다.
package dp;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class _11053{
static int n[];
static int dap=0;
static int count;
static int min=0;
static void dfs(int hgap,int flag,int depth,int dap){
if(depth == count){
min = Math.max(min, dap);
// System.out.println(min);
return;
}
// if(hgap < n[depth]){
if(flag == 1 && hgap >= n[depth]){
return;
}
else{
dfs(hgap, 0, depth + 1,dap);
dfs(n[depth], 1, depth + 1,dap+1);
}
}
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String q[] = br.readLine().split(" ");
count = Integer.parseInt(q[0]);
n = new int[1001];
q = br.readLine().split(" ");
for(int i = 0 ; i < count ; i++)
n[i] = Integer.parseInt(q[i]);
dfs(0,0,0,0);
System.out.println(min);
}
}
DFS탐색중 백트래킹으로 쓸데없는것들을 잘려버렸지만 그래도 시간초과가 되었다.
잘라내는것보다 남은것도 그렇고 dfs로 탐색하다보니 0인부분도 어쩔수없이 계산하다보니까 시간초과가 떴다.
DP를 사용하여서 할경우
S = {10,20,10,30}
일때
------------------------
(비교)
(n[i], n[j])
d[0] = 0 (0)
d[1] = 1 (10, 0)
d[2] = 1 (20, 0 => 20이 0보다 더 크니까 + 1)
d[3] = 2 (20,10 => 20이 10보다 더 크니까 +1)
d[4] = 1 (10, 0 => 10 이 더 크니까 +1을 d[0]이랑 해준다.)
d[5] = 1 (10, 10 => 10 이랑 똑같으니까 그대로)
d[6] = 1 (10, 20 => 10 이 작으니까 그대로)
d[7] = 2 (10, 20 => 10 이 작으니까 그대로)
d[8] = 1 (30, 0 => 30 이 크니까 +1)
d[9] = (30, 10 )
-------------------------
for(int i = 0 ; i < num ; i++){
}이런식으로 풀어서 다음과 같은 코드를 써봤다.
package dp;
import java.io.IOException;
import java.util.Scanner;
public class _11053 {
static int d[][];
static int n[] = new int[1001];
public static void main(String args[]) throws IOException, NumberFormatException {
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
for (int i = 1; i <= num; i++) {
n[i] = sc.nextInt();
}
// 0 10 20 30 10
d = new int[ 1 << num ][2];
int count = 1;
for (int i = 1; i <= num; i++) {
for (int j = 0; j < 1 << (i-1); j++) {
d[count][0] = n[i];
count++;
}
}
for (int i = 0; i < 1 << num; i++) {
System.out.println(d[i][0]);
}
count=1;
d[0][0] = 0;
d[0][1] = 0;
for (int i = 1; i <= num; i++) {
for (int j = 0; j < 1 << (i-1); j++) {
if (n[i] > d[j][0])
d[count][1] = d[j][1] + 1;
else
d[count][1] = d[j][1];
// System.out.print(d[count][1]);
count++;
}
// System.out.println();
}
System.out.println(d[ (1 << num) - 1][1]);
/*
6
10 20 10 30 20 50
*/
}
}메모리가 2^1001이 필요하다... 내가 잘못짠것이라고 생각이들었고 결국 풀이를 보았다.
봐도 이해가 안갔지만 결국 이해했고 LIS문제를 푸는방법은 다음과 같다.
10 20 10 30 20 50
n[i] d[i](LIS최대길이)
10 -> 1
(기본적으로 1에서 시작)
20 <=> 10
(20보다 작은것은 10이고 10의 d[0]인 1에서 +1을 진행)
10 <=> 10,20
(10보다 작은것이 없으니까 기본 1)
30 <=> 10,20,10
(30보다 작은것은 10,20,10 그러니까 d[0],d[1],d[2]에 전부 +1을 하고 그중 가장 큰값 반환
20 <=> 10,20,10,30
(20보다 작은것은 10,10 그러니까 d[0],d[2]에 +1을 하고 그중 가장 큰값 반환
50 <=> 10,20,10,30,20
(50보다 작은것은 10,20,10,30,20 그러니까 d[0]~d[4]에 +1을 하고 그중 가장 큰값을 반환
내가 생각하기에 모든 부분수열을 전부 비교하지 않는것은 이렇게 하는것이 직관적으로 더 빠르기 때문이다.
라고 생각을 해본다. 수학적 결론이라기보다는 느낌상 이렇게 하는느낌...
그래서 내가 이글 맨위에 같은 왜 이것이 답이라고 확정하거나 가장 빠른거라고 확정할수있나와 같은 생각을 한것같다.
10 - 1
20 - 2
10 - 자기(10)보다 작은값 없음 그대로 1
30 - 자기(30)보다 작은값 10,10에 +1을 하여 2,3,2중에 가장큰값인 3
20 - 자기(20)보다 작은값 10,10,에 +1을 하여 2,2중에 가장 큰값인 2
50 - 자기(50)보다 작은값 10,20,10,30,20에 +1 을 하여 2,3,2,4,3 중에 가장 큰값인 4
이중가장큰값인 4를 반환 => 정답!!!
자기보다 작은값이 없을때 그대로 1을 반환하는것의 의미 :
자기보다 작은값이 없을때 즉 10,20,10에서의 최장 길이인 부분수열은 {10,20} 이다.
즉 10보다 작다면은 해당 dp보다 길어질수 있지만 10보다 크거나 같다면 dp가 더 길어질수없기때문에
최소길이인 1로 정하는것이다.
즉 10의 d[2] = 1 에서 1이 의미하는것은 {10,20,10} 의 LIS가 1이라는것을 의미하는것이 아니라
10이라는숫자가 10앞에 있는 10,20과의 숫자보다 크지 않기 때문에 기본인 1로 두는것이다.
예를들어서 60,70,1,2,3,4 일때
60 - 1
70 - 2
1 - 1
2 - 2
3 - 3
4 - 4
와 같을때 1이랑 60,70이 1보다 크기때문에 기본인 1로 두고 시작해야지 후에 최장 길이를 비교할수가있음
package dp;
import java.io.IOException;
import java.util.Scanner;
public class _11053 {
static int d[] = new int[1001];
static int n[] = new int[1001];
public static void main(String args[]) throws IOException, NumberFormatException {
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
for (int i = 1; i <= num; i++) {
n[i] = sc.nextInt();
}
int temp;
int dap=0;
for (int i = 1; i < n.length; i++) {
temp = 1;
for (int j = 1; j < i; j++) {
if(n[i] > n[j])
temp = Math.max(d[j]+1, temp);
}
d[i] = temp;
dap = Math.max(d[i], dap);
}
System.out.println(dap);
sc.close();
}
}
이제 이것을 동적 프로그래밍인 한번구한것은 다시구하지 말자는 의미로 풀어야한다.
이대로도 답은 완성되나 n이 무수히 커질경우 시간이 매우 많이 걸린다.
이중포문의 구성이기 때문에 O(n^2)를 가진다.
그리고 이러한 의문이 생긴다. 굳이 0부터 i-1 까지 전부다 훑어야되나?
백준문제풀이Github :
https://github.com/sdk0213/baekjoon-study
sdk0213/baekjoon-study
solve a baekjoon question. Contribute to sdk0213/baekjoon-study development by creating an account on GitHub.
github.com
'Algorithm > baekjoon' 카테고리의 다른 글
| (Baekjoon) GreedyAlgorithm - (14) 반도체 설계 (0) | 2019.12.13 |
|---|---|
| (Baekjoon) dp - (7) 가장 긴 증가하는 부분 수열_O(NlogN) (0) | 2019.12.13 |
| (Baekjoon) brute-force + dp - (1) 부분수열의 합( + 부분집합 출력) (0) | 2019.12.07 |
| (Baekjoon) brute-force - (1) 부분수열의 합( + 부분집합 출력) (0) | 2019.12.07 |
| (Baekjoon) dp - (6) 타일 채우기 3 (0) | 2019.12.02 |




